Created by Rob Davidoff
GUI by Adam Schwaninger
Comments, questions, and critiques welcomed.
Introduction
WARNING! An error has been found in the calculator. The author discusses the error here. He is currently trying to diagnose the error. An update will be posted when the error is fixed.
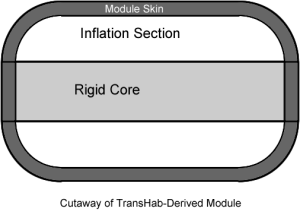
The TransHab concept was a NASA project to create an inflatable space station, which is not quite as insane as one would think. The walls include layers of Kevlar, and are probably harder to puncture than the metal walls of the International Space Station. The private company Bigelow Aerospace has purchased the rights to TransHab patents, and is in the process of developing a commercial space station. Bigelow already has launched two prototypes into orbit and they are working just fine, thank you very much.
Bimodal nuclear thermal rocket using a TransHab module for the crew compartment from Mars Reference Mission. Using the lightweight TransHab module instead of the heavier hard-shell habitat module allows re-use of the rocket on the proposed Mars mission. The hard-shell module decreases the delta-V so much that on Earth return, the crew has to bail out and be rescued while the rocket goes sailing off into the big dark with empty propellant tanks. With TransHab, there is enough delta-V so that the rocket can brake into Earth orbit and be re-used.
There are some more details about TransHab here.
Instructions
Enter in density and any two of the remaining parameters. If one of the other inputs would produce an invalid dataset when combined with one already entered, it will be greyed out.
| Furnising Level | Example | Equivalent Density |
|---|---|---|
| Basic Module | Sundancer | 47.8 kg/m^3 |
| Lightly Furnished | BA-330 | 60 kg/m^3 |
| Medium Furnishing | Habitat Unit | 100 kg/m^3 |
| Highly Furnished | Laboratory | 120 kg/m^3 |
| Basic Rigid Can | Destiny (Launch) | 118.5 kg/m^3 |
About the calculator
This calculator works via observations about the geometry of TransHab modules and the method of centroids for calculating volume.
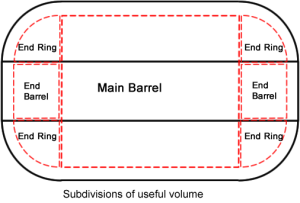
The module consists of a rigid core and an inflated bladder, which seems to generally have triple the diameter of the rigid core. This volume can be broken down further into the endcone annular portions, which are approximately quarter-circular in cross-section, the endcone barrel sections, which are rectangular in cross section, and a central barrel section, also rectangular in cross section.
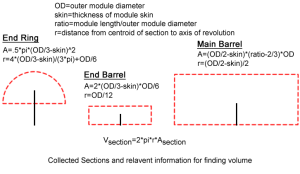
This volume can then be regrouped to produce a simpler arrangment with the same cross sectional areas and centroids. The centroid is the geometric center of ashape. For a shape like a rectangle or a circle, this is the middle point of the area. It's a bit more complicated for things like half-circles, but still can be found. Rotating this cross section around the center axis would thus yield the same volume as the TranHab module, and it turns out that the volume is equal to the area of the cross section times the distance the area's centroid travels (which is 2 times pi times the distance from the centroid to the axis of revolution for a full rotation). The geometry of module can be used to find the dimensions of each portion on this diagram (including accounting for skin thickness, which I calculate as approximately 0.3 meters) and the method of centroids used to calculate volume from that area as shown in the diagram below by summing the volume resulting from each section.
This core equation for volume is used to relate the diameter, ratio, and volume of the module. The length-to-diameter ratio is used to relate the diameter, ratio, and length of the module. The density is used to relate the mass and volume of the module. With these equations, density is always required to solve all parameters and generally two other inputs are needed, except for the following three pairings, which do are insufficient to solve for all parameters.
- Volume/Mass: over-constrains density, gives no second value for solving total volume equation to get a diameter or ratio.
- Length/Volume: gives no second value to solve to volume equation for diameter or ratio.
- Length/Mass: Density allows volume to be calculated, but then is identical to the case for Length/Volume.
Caveats
This calculator assumes that the rigid core extends only the length of the inflatable portion. This is not quite true, since some Bigelow designs include a rigid docking portion extending out from the core, but since these end portions are not conastan in size relative to the module in question, I do not calculate their volume and they are not included in the final volume or mass total. If you wish to include them, this volume is probably best approximated as a normal "rigid can" module in terms of volume and mass.
Warning
All calculated parameters are approximate. If you are using this calculator to engineer real modules: First, it's not built for that so check everything over a few times, and second, are you hiring interns?