Introduction

From Schlock Mercenary, story and artwork by Howard Tayler
Fundamentals
![]() Until we can get space industrialization cranked up to the point where we can actually build spacecraft in space, we will be stuck with constructing the blasted things in Terran-based factories and lofting them into orbit.
Until we can get space industrialization cranked up to the point where we can actually build spacecraft in space, we will be stuck with constructing the blasted things in Terran-based factories and lofting them into orbit.
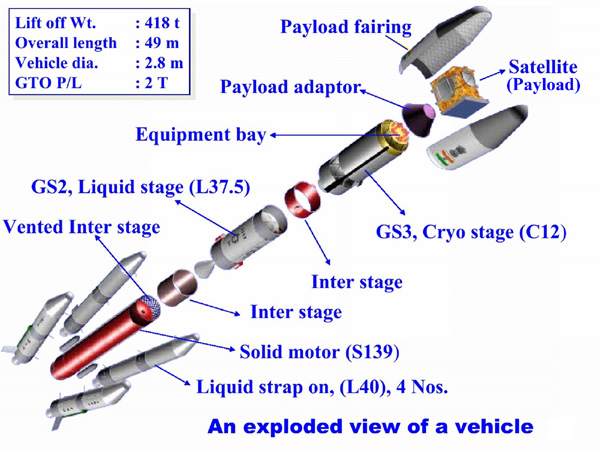
Currently we have no super-high-tech delivery systems like space elevators. So we are stuck with heavy-lift launch vehicles (HLV). These are multi-stage chemical rockets with a payload adapter on the top. The payload attaches to the adapter, and is covered by a payload fairing to protect it from being ripped to shreds by dynamic pressure and aerodynamic heating.
Once the HLV has risen above the arbitrary top of the atmosphere, the payload fairing is jettisoned (SpaceX is developing a system to reuse the faring because those suckers are hideously expensive). At the correct point in the trajectory, the payload adapter releases the payload into the desired orbit.
For Worldbuilding, get a copy of Architect of Worlds: Comprehensive Rules for Worldbuilding.
There is a limit to how big the payload faring can be. This naturally limits the size of the payload to whatever can be crammed into the faring. The faring size limits and the limits to the payload mass the HLV can boost means really large spacecraft will have to be lofted piecemeal by several HLVs and assembled in orbit. In quite a few NASA papers on Mars missions there are large sections talking about optimizing the spacecraft construction so it needs a few HLVs as possible.
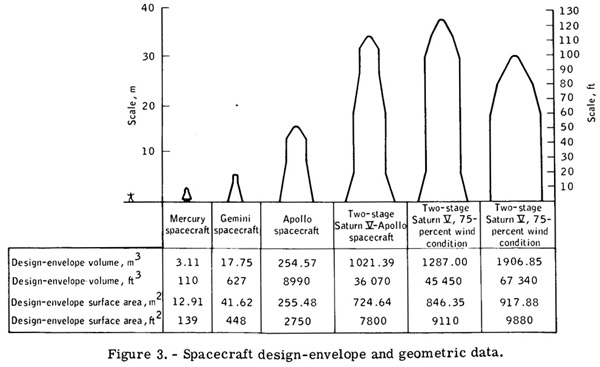
"Size" is measured by the allowable "Design envelope volume" (VT). That is, the maximum size of the spacecraft is limited to what you can cram into the payload fairing. The above graph gives some sample values of various historical spacecraft.
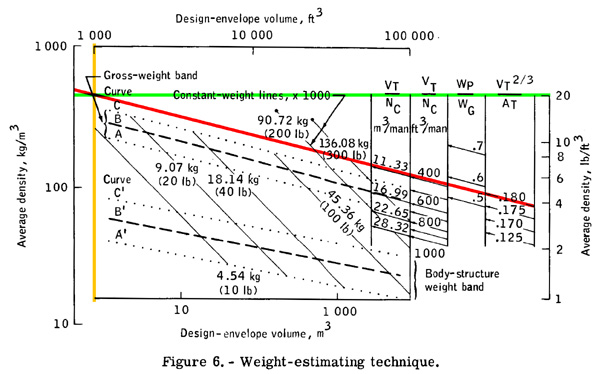
from Fundamental Techniques Of Weight Estimating And Forecasting For Advanced Manned Spacecraft And Space Stations (1971)
The above graph is for getting very rough estimates of the spacecraft. Keep in mind that it was created in 1971, using data from the currently existing NASA spacecraft of the time.
In the chart, the abscissa (horizontal axis) is the design envelope volume (m3 metric scale at bottom, stupid obsolete ft3 imperial scale at top). Ordinate (vertical axis) is the average density (kg/m3 metric scale at left, stupid obsolete lb/ft3 imperial scale at right).
Curve A is minimum density of the spacecraft's gross weight, curve B is average density, and curve C is maximum density (the three curves in the "gross weight band"). A', B', and C' are the minimum-average-maximum density of the spacecraft's body-structure (the three curves in the "body structure band").
Crew members who are crammed into a too-small habitat module tend to go stark raving insane on prolonged space missions. The chart column cryptically and sexistly labeled VT/NC m3/man is to help figure that. It is design envelope volume divided by number of crew, and is measured int cubic meters per crew person. The report is a little vague on how they calculate the number of crew. The adjacent column labeled with ft3/man is of course the stupid obsolete imperial scale.
WP/WG column is the weight of the propellant divided by the gross weight, the propellant mass fraction (Pf) in other words. The spacecraft mass ratio R is = 1 / (1+Pf)
VT2/3 / AT is the "shape factor". VT is the design envelope volume of the spacecraft, AT is the surface area. The theoretically perfect shape is a sphere, with a shape factor of 0.206. As the shape becomes increasingly less sphere-like, the value of the shape factor drops. As of 1971, manned-spacecraft bodies have shape-factor values between 0.15 and 0.18, and most aircraft bodies have shape-factor values less than 0.15. For reasons the report is vague on, the shape factor rises with gross density.