Multi-Stage - Atomic Rockets

Introduction

If your spacecraft design needs more delta-V a glance at the Tsiolkovsky rocket equation tells you you have to increase the exhaust velocity or increase the mass ratio. Or both. Since the exhaust velocity depends upon the propulsion system, often the only option is to somehow raise the mass ratio.

Staging is a desperate attempt to increase the rocket's mass ratio in order to increase the delta V to a point where the rocket can perform the desired mission. For a single stage rocket, it is very difficult to get the mass ratio above 15, and it is probably impossible to get it above 20. After all, there is only so much structural mass you can shave off before the force of acceleration will make the struts snap like toothpicks and the tanks pop like balloons.

Without staging, there is also a tendency to make huge rockets, due to the constraints of "minimum gauge".

From The Exploration of the Moon by Sir Arthur C. Clarke (1954) Artwork by R.A. Smith.
Topps "Space Cards" No. 10. (1958)
Artwork by William Hutchinson

Pournelle goes on to mention that multi stage rockets make rocket designers subconsciously think of spacecraft as "ammunition" instead of as "aircraft", that is, disposable as opposed to reusable.

By using staging, the mass ratio of the rocket as a whole can be above 15, even though the mass ratio of each individual stage is below 15. When the current lowest stage has expended all its reaction mass, that stage is discarded. This eliminates the dead weight of that stage's engines, tanks, and structural members. In essence, in a three stage rocket, stage one is a rocket who's payload is another rocket composed of stages two and three.

Back in the old days instead of the term "staging" the common term was "step rockets."

You generally only see staging in extreme circumstances, such as trying to boost a worth-while payload into Terra's orbit with anemic chemical rockets (though in Joan Vinge's THE OUTCASTS OF HEAVEN BELT there was the High Delta V Defense Force, which was an orbit to orbit flotilla of staged vehicles). You do not need staging if you are boosting payloads with atomic rockets. Nor do you need them in deep space, where you have the luxury of using those propulsion systems with high exhaust velocities (and high specific impulses) which regrettably have a thrust to weight ratio below one and thus cannot be used for lift-off.

Which is good because no self respecting Rocketeer wants to ride a disintegrating totem pole if they can possible avoid it. Not to mention the cost if the discarded stages cannot be recovered. Staging also decreases reliability, as you are multiplying the number of propulsion units that can malfunction.

In theory, one could jettison individual tanks and engines as the tanks went dry, but in practice it is more efficient to jettison an entire engine cluster. Having said that, this is the method used by the Space Shuttle with the strap on solid rocket boosters, and by the Otrag. This is called "Parallel Staging".

With staged chemical rockets, the exhaust velocity for the engines of each stage is often different. This is due to complicated optimizations that I will only lightly touch on (since I do not understand it myself). However, I get the impression that most of these optimizations only apply to lift-off, not to deep space missions.

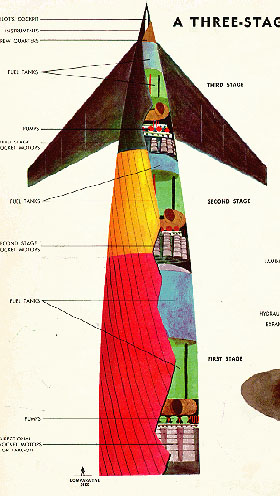
Artwork by Earl Oliver Hurst. The stage body is formed from parallel metal strips, creating the diagonal lines.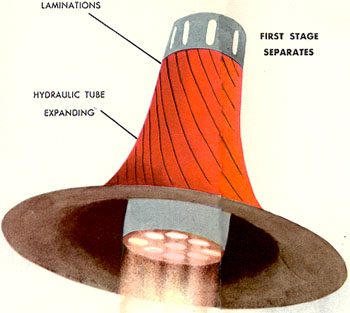
Artwork by Earl Oliver Hurst. After being jettisoned, the strips hydraulically fan out to create a rigid parachute, so the stage has a fighting chance of hitting the ground gently enough to be re-used.
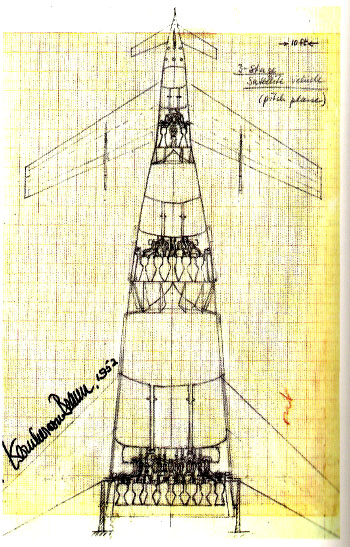
Von Braun Ferry Rocket. Click for larger image
Von Braun Ferry Rocket

From **The Outcasts of Heaven Belt** by Joan Vinge (1978)

Mass Ratio

With staging, to figure the effective mass ratio of the entire rocket, you take the individual mass ratios of each stage and multiply them. Now you know why staging is so popular with rocket scientists, despite the many draw backs.

When figuring the delta V contribution of a given stage, you use the standard delta V equation, but when figuring the mass ratio you use the total mass of the rocket after discarding the previous stage to plug into the equation.

Delta-V

Artwork by Virgil Finlay

The total delta V of the multi-stage rocket is obviously the sum of the delta V contributions of each of the stages. Since delta V is V_e * ln[R], a three stage rocket's total delta V would be:

Δ_v = (V_e1 * ln[R₁]) + (V_e2 * ln[R₂]) + (V_e3 * ln[R₃])

where

Δ_v = ship's total deltaV capability (m/s)
V_e1 = exhaust velocity of propulsion system in stage 1 (m/s)
V_e2 = exhaust velocity of propulsion system in stage 2 (m/s)
V_e3 = exhaust velocity of propulsion system in stage 3 (m/s)
R₁ = mass ratio of propellant in stage 1 to (dry mass of stage 1 plus total mass of stage 2 and 3)
R₂ = mass ratio of propellant in stage 2 to (dry mass of stage 2 plus total mass of 3)
R₃ = mass ratio of propellant in stage 3 to dry mass of stage 3

Optimization

Artwork by Virgil Finlay

Your next question is how does one determine the optimum mass ratios of each stage. I was afraid you'd ask that. It's a bit complicated. You are given the Δ_v requirements for the mission Δ_vm, and the mass of the actual mission payload (the weather satellite, the ICBM, the Apollo command and lunar module, the interplanetary warship, the orbital fighter, whatever).

To optimize a multi-stage rocket, go through the following steps, taken from the SMAD. You'll quickly discover why they call it "rocket science."

Choose the number of stages
Choose specific impulse for each stage
Choose the inert-mass fraction for each stage
Allocate a fraction of Δ_v to each stage
Size the stages and the vehicle
Minimize the vehicle mass by optimizing the Δ_v fraction alloted to each stage

Choose the number of stages

This will be called n_stage. Choose the minimum number of stages that is practical. Choose different values for n_stage and compare the marginal differences.

Choose specific impulse for each stage

The primary choice is the highest specific impulse, and if this is for lift-off you'll need a thrust to weight ratio above one.

But sometimes it is advantageous to use a propellant that has a higher density (which generally means a lower specific impulse). Sometimes if a higher density propellant is used for the lower stages, it will give you a better inert-mass fraction, which gives you a lighter first stage. But only sometimes. In other cases it may give you a lighter first stage but a heavier total vehicle mass. You will have to try and see.

Choose the inert-mass fraction for each stage

A stage's "inert mass" is the total mass of the stage minus the mass of the propellant and the mass of the payload. Inert mass is used because while we know the payload mass, we generally have no way of knowing the structural mass.

To find the "inert mass fraction", divide the inert mass by the total mass of the stage.

In existing chemical rocket designs, the inert-mass fraction of a given stage tends to be between 0.08 and 0.7.

Allocate a fraction of delta-V to each stage

The goal is to divide up the Δ_v contributions in such a way as to minimize the vehicle mass. But the only way to discover this is by trying different combinations (see step 6 below).

In the special case where each stage has the same inert-mass fractions and the same specific impulse, they will also have the same Δ_v fraction. The fraction will be 1 / n_stage. For example, if there are four stages, each stage will contribute 1/4 = 0.25 = 25% of the total Δ_v.

Size the stages and the vehicle

Start with the final (uppermost) stage and work backwards to the first stage. The payload of the uppermost stage is the actual mission payload. The payload for each lower stage includes all the previous upper stages plus the actual mission payload.

So, starting with the uppermost final stage, the payload mass is equal to the actual mission payload. The specific impulse (I_sp) for this stage comes from step 2. The inert-mass fraction (f_inert) for this stage comes from step 3. And the Δ_v fraction (f_{Δ_v}) for this stage comes from step 4.

Using those values, we can calculate the propellant mass, the inert mass, and the initial mass of that stage.

To calculate the propellant mass: specific Impulse gives us the Exhaust Velocity:

V_e = g₀ * I_sp

Δ_v fraction and mission Δ_v gives us the stage Δ_v:

Δ_vs = f_{Δ_v} * Δ_vm

Δ_vs and Exhaust Velocity gives us the Mass Ratio:

R = e^(Δ_vs/V_e)

Payload mass, mass ratio, and inert mass fraction gives us the Mass of the Propellant:

M_pt = (M_pl * (R-1) * (1 - f_inert)) / (1 - (f_inert * R))

where:

V_e = Exhaust velocity (m/s)
Δ_vm = total mission Δ_v
f_{Δ_v} = Δ_v fraction for this stage
Δ_vs = Δ_v for this stage
g₀ = Acceleration due to gravity at Earth's surface = 9.81 (m/s²)
I_sp = Specific impulse (s)
e^x = the inverse of the Ln() function, called "exp(x)" in spreadsheets
f_inert = inert-mass fraction
M_pl = mass of "payload" (kg)
M_pt = mass of propellant (kg)

To calculate the inert mass:

M_inert = (f_inert / (1 - f_inert)) * M_pt

Finally, to calculate the initial mass of the stage:

M = M_pl + M_pt + M_inert

For the next lower, and all subsequently lower stages, use the value of the previous stage's initial mass M in the place of the payload mass M_pl, use the new stage's values for Δ_v fraction, specific impulse, and inert-mass fractions. Re-calculate all the equations with the new values.

Keep doing this until you have finished all the stages. The initial mass M of the last stage is the vehicle's initial mass. The goal is to get the vehicle's initial mass to be as low as possible.

Minimize the vehicle mass by optimizing the delta-V fraction alloted to each stage

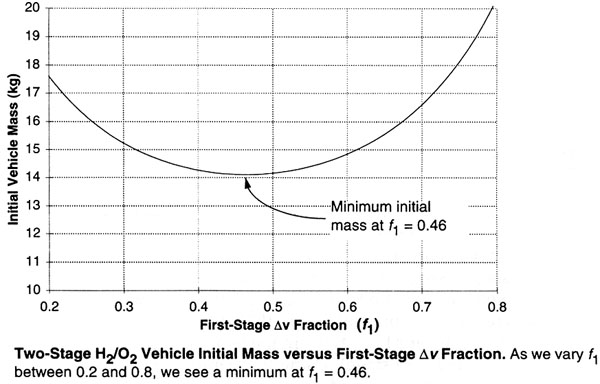
Graph from Space Mission Analysis and Design (1999).

The Δ_v fractions of each of the stages must be varied in order to determine the combination that minimizes the vehicle's initial mass. This generally is done with an "iterative process," i.e., a computer program, a grad student, or unlucky you has to repeatedly run various combinations of Δ_v fractions through steps 4 and 5 until the minimum initial mass is discovered.

With a two stage rocket, it is, well, I won't say "easy" but it is a lot easier than a three or more stage rocket. Obviously with a two stage rocket, once you've decided on a value for the Δ_v fraction of stage one, you have automatically determined stage two's Δ_v fraction (i.e., it is 1.0 - f_{Δ_v1}).

So you set a range of values for the Δ_v fraction of stage one (say, from 0.2 to 0.8) and step through it at convenient intervals (say, increment by 0.1 each step). Subtract from 1.0 to figure the fraction for stage two. Send these through the battery of equations above and plot them on a graph like this:

By inspecting the graph, you can identify the minimum value for initial vehicle mass, and the associated Δ_v fractions. Your optimization is complete.

Performing this for three or more stages is a major pain in the gluteus maximus.

We need to vary two Δ_vs over some range to find a minimum. For a three stage system, we repeat the above graphing technique for a range of f_{Δ_v2} values, choosing the minimum f_{Δ_v1} value for each f_{Δ_v2} (remember f_{Δ_v3} = 1.0 - f_{Δ_v1} - f_{Δ_v2}). We can then plot the initial vehicle mass (each point being minimized for f_{Δ_v1}) and choose the f_{Δ_v2} with the minimum initial mass value.