Starmap Main > Stereo Starmaps

ρ=Σ+Ψ


|
Stories of the Stars: Antares. Artwork by Frank Paul
|
 It is rather anticlimatic
to go to all the trouble of calculating the three-dimensional co-ordinates
of one's starmap, only to use it to create a flat-as-a-pancake printed
map. But you brave souls who aren't afraid of some more math can use the
following information to make your maps explode into the third dimension! It is rather anticlimatic
to go to all the trouble of calculating the three-dimensional co-ordinates
of one's starmap, only to use it to create a flat-as-a-pancake printed
map. But you brave souls who aren't afraid of some more math can use the
following information to make your maps explode into the third dimension!
|
I forsee two main uses of the following equations:
-
 Rotatable Maps
Rotatable Maps
-
This is a computer program capable of displaying a starmap on the monitor,
and allowing the user to spin the map around its center in various directions
in order to see the stellar arrangements. This is used in the MacSpin
demo and the NearStar program.
-
 Stereo Twin Maps
Stereo Twin Maps
-
A map, either on the computer or printed, which when viewed in the proper
manner presents the illusion of a three-dimensional object. There are many
techniques, but all are based on the idea of presenting one eye with one
picture, and the other with a slightly different picture.
-
 Stereo Twins
Stereo Twins
-
Pairs of pictures which can be viewed by crossing one's eyes,
"wide-eyed" viewing, or inserting the pictures into a stereoptican, ViewMaster,
military surplus stereoscope, or similar device. If you need help learning
how to view these images, go here.
The images below were created with my source code
below.
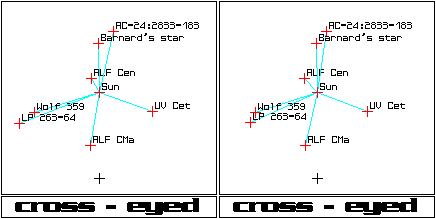
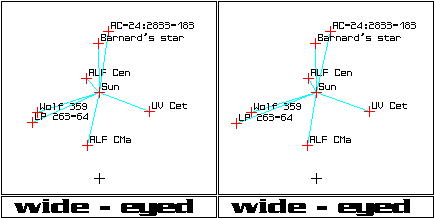
-
 Anaglyphs
Anaglyphs
-
Pairs of pictures are printed one on top of the other, one in
blue ink, the other in red. Glasses with one red lens and one blue are
used to view the image. Some movies use this technique using two projectors,
each with a polarizing filter oriented at ninety degrees to the other.
Polaroid glasses with the two lenses at ninety degrees to each other are
used to view. Here is an
anaglyph I whipped up, showing all the stars in the Gliese 3.0 catalog
within 5.0 parsecs in equatorial co-ordinates, with lines drawn between
stars closer than 2.0 parsecs. Here are
some anaglyphs based on the Hipparcos catalog. (Please note that they are
printed sideways). Thanks to James
Fowler for bringing these to my attention. Also, check out the book
3-D
starmaps for more anaglyphs. Reel
3-D Enterprises can supply you with red-blue
anaglyph glasses, as well as a nifty book
on how to draw anaglyphs with colored pencils. Rainbow
Symphony has a wide selection of 3-D glasses, as does 3-D
Glasses Direct. Or go here
for a "free" set of anaglyph glasses. The image below was created with
black and white version of the above stereo pairs, and merged with Adobe
Photoshop.
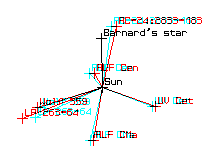
(red lens on left eye)
-
 "Magic Eye" Stereograms
"Magic Eye" Stereograms
-
The pairs of pictures are merged in patterns of random dots. This
is not very well suited for starmaps, as the pictures are very grainy.
-
 Liquid Crystal Shutter Goggles
Liquid Crystal Shutter Goggles
-
This uses very expensive hardware, but it quite striking. A computer
is programmed to alternate between two images displayed on the monitor,
alternating very rapidly (tens of cycles per second). Special liquid crystal
goggles are capable of alternately blacking out one eye, then the other,
in synch with the monitor. Chances are, if you own such equipment, you
either know the following equations already, or have access to software
that will do the job for you. If you are interested in this equipment,
check out Christoph Bungert's mavelous Stereoscopic
3D Homepage.
Of course, I'm sure that some of you fiendishly clever starmappers out
there will come up with other uses for this stuff!
 Brace yourselves...
Brace yourselves...
Now comes tons of complicated and confusing equations! I'll try to make
this as simple as possible. And I trust you will forgive me if I concentrate
on the equations proper and totally ignore such nicieties as the derivation
of said equations, why they work, and similar issues. (Translation: I personally do not
know how to derive them, nor why they work) I'm sure that the interested
reader can find entire textbooks on the subject.
Also note that I could have made serious mistakes in the following
exposition due to my unfamiliarity with the subject matter. Use these equations
at your own risk, and please email me if you spot an error!
 Pesky definitions
Pesky definitions
 WORLD CO-ORDINATES: We
start with a list of all the stars that you have painstakingly translated
into x,y, and z co-ordinates. We are going to refer to these as being in
World
co-ordinates. The x-y plane is horizontal, with the positive z co-ord extending
upward
WORLD CO-ORDINATES: We
start with a list of all the stars that you have painstakingly translated
into x,y, and z co-ordinates. We are going to refer to these as being in
World
co-ordinates. The x-y plane is horizontal, with the positive z co-ord extending
upward
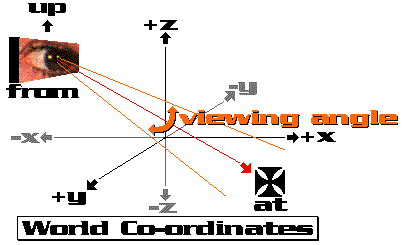
 FROM: Next, we choose
a point where our eye will be mathematically located. Typically this will
be user settable by the program incorporating these equations. This will
be refered to as the From point, located at FromX, FromY, FromZ
in World co-ordinates. In order to make a starmap spin, you will have to
incorporate some method of allowing the From point to orbit the starmap.
Note that for creating a stereo twin pictures as opposed to a rotatable
starmap, one will have to have two sets of From points, one for each eye.
The magical equations will have to be run on each star point twice, once
for the left eye, once for the right. The distance between the two From
points should be about the same as the distance between the centers of
your
eyes, i.e., about three inches or seven centimeters, measured in screen
pixel units or whatever your printed map scale is.
FROM: Next, we choose
a point where our eye will be mathematically located. Typically this will
be user settable by the program incorporating these equations. This will
be refered to as the From point, located at FromX, FromY, FromZ
in World co-ordinates. In order to make a starmap spin, you will have to
incorporate some method of allowing the From point to orbit the starmap.
Note that for creating a stereo twin pictures as opposed to a rotatable
starmap, one will have to have two sets of From points, one for each eye.
The magical equations will have to be run on each star point twice, once
for the left eye, once for the right. The distance between the two From
points should be about the same as the distance between the centers of
your
eyes, i.e., about three inches or seven centimeters, measured in screen
pixel units or whatever your printed map scale is.
 AT: Now, we choose
a point that our eye is looking at, the At point. Generally this
will be the center of the starmap, which will generally be at 0,0,0 in
World co-ordinates. AtX = 0, AtY = 0, AtZ = 0. For two eyes, the At point
is the same
AT: Now, we choose
a point that our eye is looking at, the At point. Generally this
will be the center of the starmap, which will generally be at 0,0,0 in
World co-ordinates. AtX = 0, AtY = 0, AtZ = 0. For two eyes, the At point
is the same
 UP: Next, we need
an Up point, which points in the eye's "upward" direction. For now,
just set UpX = 0, UpY = 0, and UpZ = 1.
UP: Next, we need
an Up point, which points in the eye's "upward" direction. For now,
just set UpX = 0, UpY = 0, and UpZ = 1.
 THETA: Finally we
need Theta, the "viewing angle". This defines the cone of vision.
Use 60 degrees for now. Other values can give a fisheye lense effect. Don't
forget to convert the angle into radians if your programming language demands
it. Multiply degrees by 0.017453293 to convert to radians.
THETA: Finally we
need Theta, the "viewing angle". This defines the cone of vision.
Use 60 degrees for now. Other values can give a fisheye lense effect. Don't
forget to convert the angle into radians if your programming language demands
it. Multiply degrees by 0.017453293 to convert to radians.
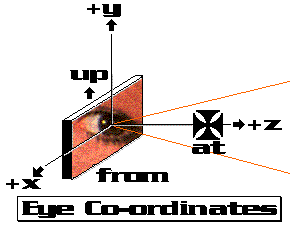
 EYE CO-ORDINATES:
In the first step below, we will be converting World co-ords into Eye
co-ords. In this co-ordinate system, the eye is at the origin, the positive
Y axis will point upward, in the direction of the Up point, the positive
X axis will point to the right, and the positive Z axis will extend into
the screen going away from you, with the At point on the Z axis.
EYE CO-ORDINATES:
In the first step below, we will be converting World co-ords into Eye
co-ords. In this co-ordinate system, the eye is at the origin, the positive
Y axis will point upward, in the direction of the Up point, the positive
X axis will point to the right, and the positive Z axis will extend into
the screen going away from you, with the At point on the Z axis.
 Now, wasn't that easy?
Now, wasn't that easy?
Here are the steps you need to do on each star in order to determine the
screen or print-out co-ordinates. Again, remember that if you are creating
a stereo twin picture as opposed to a rotatable starmap, one will have
to run these steps twice, once for each eye.
-
[1] Convert World co-ords into Eye co-ords
-
[1A] Make From point the origin
-
[1B] Rotate X axis so At point lies on positive Z axis
-
[1C] Rotate Y axis in the same way
-
[1D] Rotate Z axis
-
[2] Perspective Transformation
After this it is up to you to display your data. For a Rotatable map, draw
it on the monitor. For Stereo Twins, draw the data from the Left Eye in
the left half of the screen/paper and the data from the Right Eye in the
right half (for the wide-eyed method. For the cross-eyed method swap the
halves). For Anaglyphs, print boths sets of data on top of each other,
in colors based on the goggles. The right map color should be invisible
through the left color goggle and vice versa.
 Well,
I guess it wasn't so easy after all!
Well,
I guess it wasn't so easy after all!
Calculating steps 1A through 1D take an awful lot of calculations. The
pros use the miracle of Matrix Algebra in order to combine all these
into a handful of calculations.
Don't worry, I'll just show the details of the matrix for those who
have the knowledge and the interest in it. The rest of us can skip
down to the application of said matrix.
Step 1A is pretty simple:
FCenterX = starX - FromX
FCenterY = starY - FromY
FCenterZ = starZ - FromZ
This changes the co-ords from World co-ords to World co-ords with the
From point at the origin. (note that the above is for illustration only,
we won't be using those equations in that form in our actual algorithm)
Now, don't panic, but here's the matrix that combines steps 1B, 1C,
and 1D:
+- -+
| a1x a2x a3x 0 |
| |
| a1y a2y a3y 0 |
V = | |
| a1z a2z a3z 0 |
| |
| 0 0 0 1 |
+- -+
(A1) (A2) (A3)
To compute A1, A2, a' = At - From.
A1 = (a' x Up) / ||a' x Up||
A2 = ((a' x Up) x a') / ||(a' x Up) x a'||
A3 = a' / ||a'||
where
x = the cross product of two vectors
|| z || = the magnitude of z
No, I'm not going to explain what those operation are.
Step 2 is also simple:
ScreenX = (EyeX * D) / EyeZ
ScreenY = (EyeY * D) / EyeZ
Where D is the distance from the eye to the viewing plane, and
is calculated from Theta. D = COS(Theta/2) / SIN(Theta/2)
This is just the fundamental law of perspective: The farther away
it is from you, the smaller it appears. In this case, we are scaling it
to go closer to the center of the screen, which is centered on At, the
vanishing point.
Since we've gotten that out of the way, I'll now
show you how to do steps 1A-2 in a form suitable for programming. Note
that the text in {italics} are comments, and are not part of the
algorithm.
{As an example, when FromX,Y,Z is for the left eye, set it
to -0.5,0,10
and +0.5,0,10 for the right eye. This puts the eyes hovering 10
units over the
x-y plane, with the two eyes separated by 1.0 unit}
FromX = {user input}
FromY = {user input}
FromZ = {user input}
AtX = 0
AtY = 0
AtZ = 0
{ we are looking down at the map on the table, so "up" is in the
+Y direction}
UpX = 0
UpY = 1
UpZ = 0
Theta = 60 * 0.017453293
DVal = COS(Theta / 2) / SIN(Theta / 2)
{ Compute a' }
aPrimeX = AtX - FromX
aPrimeY = AtY - FromY
aPrimeZ = AtZ - FromZ
{ Compute ||a'|| }
aPrimeMag = SQRT((aPrimeX^2) + (aPrimeY^2) + (aPrimeZ^2))
{ Fill the A3 section of the matrix with A3 = a' / ||a'|| }
A3X = aPrimeX / aPrimeMag
A3Y = aPrimeY / aPrimeMag
A3Z = aPrimeZ / aPrimeMag
{ Compute a' x Up }
TempX = (aPrimeY * UpZ) - (UpY * aPrimeZ)
TempY = (aPrimeZ * UpX) - (UpZ * aPrimeX)
TempZ = (aPrimeX * UpY) - (UpX * aPrimeY)
{ Compute ||a' x Up|| }
TempMag = SQRT((TempX^2) + (TempY^2) + (TempZ^2))
{ Fill the A1 section of the matrix with A1 = (a' x Up) / ||a' x
Up|| }
A1X = TempX / TempMag
A1Y = TempY / TempMag
A1Z = TempZ / TempMag
{ Compute (a' x Up) x a' }
TempX = (A1Y * A3Z) - (A3Y * A1Z)
TempY = (A1Z * A3X) - (A3Z * A1X)
TempZ= (A1X * A3Y) - (A3X * A1Y)
{ Compute ||(a' x Up) x a'|| }
TempMag = SQRT((TempX^2) + (TempY^2) + (TempZ^2))
{ Fill the A2 section of the matrix with A2 = ((a' x Up) x a') /
||(a' x Up) x a'|| }
A2X = TempX / TempMag
A2Y = TempY / TempMag
A2Z = TempZ / TempMag
{ Compute offset for Step 1A }
OffX = -(A1X * FromX)-(A1Y*FromY)-(A1Z*FromZ)
OffY = -(A2X * FromX)-(A2Y*FromY)-(A2Z*FromZ)
OffZ = -(A3X * FromX)-(A3Y*FromY)-(A3Z*FromZ)
{ Initialization is finished. Now, for each StarX,StarY,StarZ, do
the following: }
{ Convert star's World co-ords into Eye co-ords (steps 1A-1D) }
EyeX = (StarX * A1X) + (StarY * A1Y) + (StarZ * A1Z ) + OffX
EyeY = (StarX * A2X) + (StarY * A2Y) + (StarZ * A2Z ) + OffY
EyeZ = (StarX * A3X) + (StarY * A3Y) + (StarZ * A3Z ) + OffZ
{ Calculate perspective transform (step 2) }
ScreenX = (EyeX * DVal) / EyeZ
ScreenY = (EyeY * DVal) / EyeZ
Plot the star. Now do the next one.
When done, set FromX,Y,Z to the other eye, and do it all again.
Here is a code fragment
written in C implementing the above algorithm. You will have to change
it a bit to make it work with your program (adding DeviceContexts to the
"MoveTo" and "LineTo" commands if you are programming in Windows, etc.)
Again, I cannot guarantee that the above is error free. Beware. But
have fun!
+=======================(:)=== ^ ===(:)======================================+
| WINCHELL CHUNG |=| /_\ |=| I'm nobody. Nobody at all. But the |
|Nyrath the nearly wise |\| <(*)> |\| secrets of the universe don't mind. |
| nyrath@projectrho.com |=| /_/|\_\ |=| They reveal themselves to nobodies |
| |\| //|\\ |\| that care. OUTER LIMITS: Galaxy Being|
+=======================(:)=///|\\\=(:)======================================+
![[Winchell Photo]](winch8xs.gif) Back
to The Weird World of Winchell Chung
Back
to The Weird World of Winchell Chung
 Send all questions, comments, and sarcastic remarks to:
Send all questions, comments, and sarcastic remarks to:





![]() FROM: Next, we choose
a point where our eye will be mathematically located. Typically this will
be user settable by the program incorporating these equations. This will
be refered to as the From point, located at FromX, FromY, FromZ
in World co-ordinates. In order to make a starmap spin, you will have to
incorporate some method of allowing the From point to orbit the starmap.
Note that for creating a stereo twin pictures as opposed to a rotatable
starmap, one will have to have two sets of From points, one for each eye.
The magical equations will have to be run on each star point twice, once
for the left eye, once for the right. The distance between the two From
points should be about the same as the distance between the centers of
your
eyes, i.e., about three inches or seven centimeters, measured in screen
pixel units or whatever your printed map scale is.
FROM: Next, we choose
a point where our eye will be mathematically located. Typically this will
be user settable by the program incorporating these equations. This will
be refered to as the From point, located at FromX, FromY, FromZ
in World co-ordinates. In order to make a starmap spin, you will have to
incorporate some method of allowing the From point to orbit the starmap.
Note that for creating a stereo twin pictures as opposed to a rotatable
starmap, one will have to have two sets of From points, one for each eye.
The magical equations will have to be run on each star point twice, once
for the left eye, once for the right. The distance between the two From
points should be about the same as the distance between the centers of
your
eyes, i.e., about three inches or seven centimeters, measured in screen
pixel units or whatever your printed map scale is.
![]() AT: Now, we choose
a point that our eye is looking at, the At point. Generally this
will be the center of the starmap, which will generally be at 0,0,0 in
World co-ordinates. AtX = 0, AtY = 0, AtZ = 0. For two eyes, the At point
is the same
AT: Now, we choose
a point that our eye is looking at, the At point. Generally this
will be the center of the starmap, which will generally be at 0,0,0 in
World co-ordinates. AtX = 0, AtY = 0, AtZ = 0. For two eyes, the At point
is the same
![]() UP: Next, we need
an Up point, which points in the eye's "upward" direction. For now,
just set UpX = 0, UpY = 0, and UpZ = 1.
UP: Next, we need
an Up point, which points in the eye's "upward" direction. For now,
just set UpX = 0, UpY = 0, and UpZ = 1.
![]() THETA: Finally we
need Theta, the "viewing angle". This defines the cone of vision.
Use 60 degrees for now. Other values can give a fisheye lense effect. Don't
forget to convert the angle into radians if your programming language demands
it. Multiply degrees by 0.017453293 to convert to radians.
THETA: Finally we
need Theta, the "viewing angle". This defines the cone of vision.
Use 60 degrees for now. Other values can give a fisheye lense effect. Don't
forget to convert the angle into radians if your programming language demands
it. Multiply degrees by 0.017453293 to convert to radians.
![]() EYE CO-ORDINATES:
In the first step below, we will be converting World co-ords into Eye
co-ords. In this co-ordinate system, the eye is at the origin, the positive
Y axis will point upward, in the direction of the Up point, the positive
X axis will point to the right, and the positive Z axis will extend into
the screen going away from you, with the At point on the Z axis.
EYE CO-ORDINATES:
In the first step below, we will be converting World co-ords into Eye
co-ords. In this co-ordinate system, the eye is at the origin, the positive
Y axis will point upward, in the direction of the Up point, the positive
X axis will point to the right, and the positive Z axis will extend into
the screen going away from you, with the At point on the Z axis.
