Nomography Main > Determinant 5

ρ=Σ+Ψ
Functional Moduli
So you finally have your determinant for your nomogram. Now you need to
add the Functional Moduli ( Scale Factors ) to the
Basic Determinant in order to create the Constructional Determinant. This
is already done for you for the basic nomograms in the cheat sheets.
If your nomogram is not in the list, you have to create the Constructional Determinant yourself.
Why does one want to mess with Functional Moduli? Mainly to adjust the size of the scales
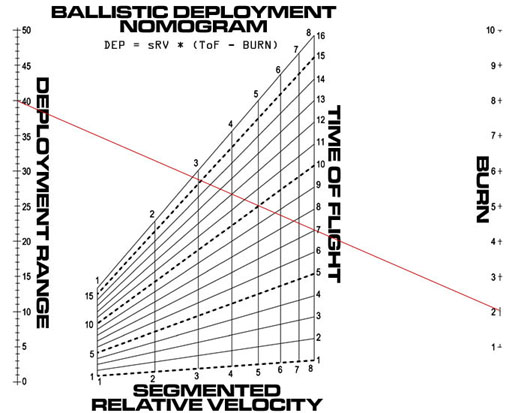
for maximum accuracy. For example this nomogram is plotted with no functional moduli:
Note how tiny the "Burn" scale is. This hurts accuracy. What we want is for the
"Burn" scale and the "Deployment Range" scale to be roughly the same size.
By using a large functional modulus for that scale, we get this:
Much better accuracy.
First one has to know how to multiply two determinants together:
| x1 |
y1 |
z1 |
| x2 |
y2 |
z2 |
| x3 |
y3 |
z3 |
|
* |
| a1 |
b1 |
c1 |
| a2 |
b2 |
c2 |
| a3 |
b3 |
c3 |
|
| = |
| a1x1 + a2y1 + a3z1 |
b1x1 + b2y1 + b3z1 |
c1x1 + c2y1 + c3z1 |
| a1x2 + a2y2 + a3z2 |
b1x2 + b2y2 + b3z2 |
c1x2 + c2y2 + c3z2 |
| a1x3 + a2y3 + a3z3 |
b1x3 + b2y3 + b3z3 |
c1x3 + c2y3 + c3z3 |
|
But don't panic. Generally you won't be doing the entire thing, just a part of it. Consider the above
to be a cheat sheet used to figure what goes where in your specific determinant.
If you simply must know how it is done: the element in the i-th row and the
j-th column of the product determinant is the sum of the products obtained by
multiplying each element of the i-th row of the first factor by the corresponding
element of the j-th column of the second factor. But you don't have to know that
if you have the cheat sheet.
Lets insert functional moduli into the determinant for P + Q - R = 0.
Inserting the equation into a determinant gives us:
Converted into Basic Nomographic Form using the Four Rules:
What we need to do is construct a Transformational Determinant. This
will be multiplied with the Basic Determinant in order to create the
Constructional Determinant.
Lets say that we have decided that the Q scale should be
unchanged. This means that x1
and z1 (i.e., Q and 1)
both have to be multiplied by 1 (since y1
is zero we don't care what it is multiplied with). Glancing at the
cheat sheet, we see that we have to put 1 in a1
for Q and a 1 in c3 for the 1 in z1.
Zeroes have to be added to cancel unwanted factors. So far our transformation looks like:
| = |
| 1Q + ?0 + 0*1 |
0Q + ?0 + 0*1 |
0Q + ?0 + 1*1 |
| 1P + ?1 + 0*1 |
0P + ?1 + 0*1 |
0P + ?1 + 1*1 |
| 1(0.5R) + ?(0.5) + 0*1 |
0(0.5R) + ?(0.5) + 0*1 |
0(0.5R) + ?(0.5) + 1*1 |
|
| = |
| Q |
0 |
1 |
| P + ? |
? |
? + 1 |
| (0.5R) + ?(0.5) |
?(0.5) |
?(0.5) + 1 |
|
The scales P and R will be changed in length and position, but they
are to remain parallel to each other (since this is a parallel scale chart)
So a2, b2, and c2
will be our functional moduli.
| = |
| 1Q + a20 + 0*1 |
0Q + b20 + 0*1 |
0Q + c20 + 1*1 |
| 1P + a21 + 0*1 |
0P + b21 + 0*1 |
0P + c21 + 1*1 |
| 1(0.5R) + a2(0.5) + 0*1 |
0(0.5R) + b2(0.5) + 0*1 |
0(0.5R) + c2(0.5) + 1*1 |
|
| = |
| Q |
0 |
1 |
| P + a2 |
b2 |
c2 + 1 |
| 0.5(R + a2) |
0.5b2 |
0.5c2 + 1 |
|
All this transformation has messed things up, so convert
into Basic Nomographic Form using the
Four Rules
| Q |
0 |
1 |
| ( P + a2 ) / ( c2 + 1 ) |
b2 / ( c2 + 1 ) |
1 |
| ( R + a2 ) / ( c2 + 2 ) |
b2 / ( c2 + 2 ) |
1 |
|
= 0 |
And that's our Constructional Determinant.
If you want the ultimate in control you can try this technique from
Fundamental Formulas of Physics, Vol. 1. Say that you have a determinant in
three variables
a,
b, and
g.
| f1(a) |
y1(a) |
1 |
| f2(b) |
y2(b) |
1 |
| f3(g) |
y3(g) |
1 |
|
= 0 |
You can control every single aspect of the appearance of the nomogram with
nine functional moduli a, b, c, d, e, f, g, h, and i.
|
( af1 + by1 + c ) /
( gf1 + hy1 + i )
|
( df1 + ey1 + f ) /
( gf1 + hy1 + i )
|
1 |
|
( af2 + by2 + c ) /
( gf2 + hy2 + i )
|
( df2 + ey2 + f ) /
( gf2 + hy2 + i )
|
1 |
|
( af3 + by3 + c ) /
( gf3 + hy3 + i )
|
( df3 + ey3 + f ) /
( gf3 + hy3 + i )
|
1 |
|
= 0 |
By manipulating these nine moduli one can control the position and size of the three scales.
Two of the constants fix the scales of the x and y. Two more determine the choice of origin.
Four more defines a line on the plane and the remaining moduli defines the degree of
rotation of the diagram around the line as an axis. However I am unsure as to
which moduli does what so you will have to experiment yourself.