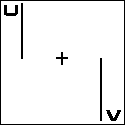Nomography Main > Standard Forms of the Third Class

ρ=Σ+Ψ
Standard Forms of the Third Class
i.e., Cheat Sheets
Note: If this "r=S+Y" is not composed of
letters of the Greek alphabet, you probably have Netscape 6+ or Mozilla.
You can enable the font with instructions found here.
These tables are taken from The Nomogram: The Theory And Practical Construction Of Computational Charts
by H.J. Allcock and J.R. Jones (1946). They are for nomograms of equations with three variables
(u,v,w).
If you can reduce your equation to one resembling an entry in these tables you will
save yourself an awful lot of work. Note that while these are only good for equations of
three variables, it is possible to use them for a three variable component of
a mult-variable nomogram.
If you cannot reduce your equation, I'm sorry, you are going to have to do it the hard way.
δ1,
δ3,
μ1, and
μ3 are
functional moduli (scaling values).
In a spreadsheet you will alter these values by hand until the nomogram looks best.
The "Class" of a nomogram is the number of variables in the equation it solves for,
all the nomograms on this page are of Class 3. The "Genus" of a nomogram is the number
of functions in the equation minus the number of variables. So a nomogram of the equation
f(u) - { { g(v) . f(w) - f(v) . g(w) } / { g(v) - g(w) } } = 0 has a Class of 3
(for u, v, and w) and a Genus of 2 (f(u), f(v), f(w), g(v), g(w) is five functions, minus three is Genus 2)
GENUS 0
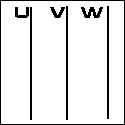
f(u) + f(v) + f(w) = 0 Parallel Scale Nomogram U + V = W
Basic
Determinant |
|
Constructional
Determinant |
|
|
| -1 | f(u) | 1 |
| 0 | -1/2 f(v) | 1 |
| 1 | f(w) | 1 |
|
=0 |
| -δ1 |
μ1 . f(u) |
1 |
| 0 |
-{{μ1 . μ3} / {μ1+μ3}} . f(v) |
1 |
| δ3 |
μ3 . f(w) |
1 |
|
=0 |
 |
|
|
where δ1
.μ3
=δ3
.μ1 or |
|
| -δ1 |
{ 1/δ3 } . f(u) |
1 |
| 0 |
-{ 1 / { δ1 + δ3 }} . f(v) |
1 |
| δ3 |
{ 1/δ1 } . f(w) |
1 |
f(w) + f(v) . f(w) - k . f(v) - f(u) . f(v) = 0
Basic
Determinant |
|
Constructional
Determinant |
|
| 0 | f(u) | 1 |
| f(v) | k . f(v) | 1 |
| 1 | f(w) | 1 |
|
=0 |
| 0 |
μ1 . f(u) |
1 |
{δ3 . μ1 . f(v)} /
{{μ1 - μ3}f(v) + μ3}
|
{μ1 . μ3 . k . f(v)} /
{{μ1 - μ3}f(v) + μ3}
|
1 |
| δ3 |
μ3 . f(w) |
1 |
|
=0 |
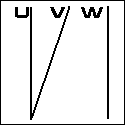 |
f(v) - { f(u) / { f(u) + f(w) } } = 0
Basic
Determinant |
|
Constructional
Determinant |
|
|
|
=0 |
| 0 |
μ1 . f(u) |
1 |
{δ3 . μ1 . f(v)} /
{{μ1 - μ3}f(v) + μ3}
|
0 |
1 |
| δ3 |
-μ3 . f(w) |
1 |
|
=0 |
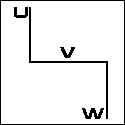 |
f(v) - { f(u) / f(w) } = 0 The "N" or "Z" Nomogram U / W = V
Basic
Determinant |
|
Constructional
Determinant |
|
| 0 | f(u) | 1 |
| f(v) / { f(v) + 1} | 0 | 1 |
| 1 | -f(w) | 1 |
|
=0 |
| 0 |
μ1 . f(u) |
1 |
{δ3 . μ1 { f(v) / { f(v)+1} } } /
{{μ1 - μ3}{ f(v) / { f(v)+1} } + μ3}
|
0 |
1 |
| δ3 |
-μ3 . f(w) |
1 |
|
=0 |
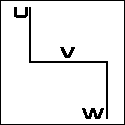 |
f(v) - { { f(u) . f(w) } / { f(u) + f(w) } } = 0 The Concurrent-scale nomogram
Basic
Determinant |
|
Constructional
Determinant |
|
|
|
=0 |
| δ1 . f(u) |
0 |
1 |
| δ1 . f(v) |
μ3 . f(v) |
1 |
| 0 |
μ3 . f(w) |
1 |
|
=0 |
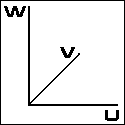 |
f(u) + { { f(w){ f(v)+k1 }} / { { f(v) + k2 } - f(w)}} = 0
Basic
Determinant |
|
Constructional
Determinant |
|
| f(u) | 0 | 1 |
| f(v) + k1 | f(v) + k2 | 1 |
| 0 | f(w) | 1 |
|
=0 |
| δ1 . f(u) |
0 |
1 |
| δ1{ f(v) + k1 } |
μ3{ f(v) + k2 } |
1 |
| 0 |
μ3 . f(w) |
1 |
|
=0 |
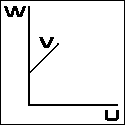 |
f(u) = f(v) Expanded Two Variable Nomogram
Basic
Determinant |
|
Constructional
Determinant |
|
|
|
=0 |
| -δ1 |
μ1 . f(u) |
1 |
| 0 |
0 |
1 |
| δ3 |
-μ3 . f(v) |
1 |
|
=0 |
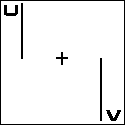 |
|
|
where
δ1
.μ3
=δ3
.μ1 |
|
GENUS I
f(u) - f(v) + g(v){ f(w) - f(u)} = 0
Basic
Determinant |
|
Constructional
Determinant |
|
|
|
=0 |
| 0 |
μ1 . f(u) |
1 |
{ δ3 . μ1 . g(v) } /
{ { μ1 - μ3 }g(v) + μ3 }
|
{ μ1 . μ3 . f(v) } /
{ { μ1 - μ3 }g(v) + μ3 }
|
1 |
| δ3 |
μ3 . f(w) |
1 |
|
=0 |
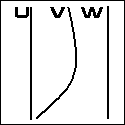 |
f(u) . f(v) + g(v) . f(w) - f(w) . f(u) = 0
Basic
Determinant |
|
Constructional
Determinant |
|
|
|
=0 |
| δ1 . f(u) |
0 |
1 |
| δ1 . g(v) |
μ3 . f(v) |
1 |
| 0 |
μ3 . f(w) |
1 |
|
=0 |
 |
GENUS II
f(u) - { { g(v) . f(w) - f(v) . g(w) } / { g(v) - g(w) } } = 0
Basic
Determinant |
|
Constructional
Determinant |
|
| 0 | f(u) | 1 |
| g(v) | f(v) | 1 |
| g(w) | f(w) | 1 |
|
=0 |
| 0 |
μ1 . f(u) |
1 |
| δ3 . g(v) |
μ1 . f(v) |
1 |
| δ3 . g(w) |
μ1 . f(w) |
1 |
|
=0 |
 |
GENUS III
g(u){ f(v) - f(w) } + g(v){ f(w) - f(u) } + g(w){ f(u) - f(v) } = 0
Basic
Determinant |
|
Constructional
Determinant |
|
| g(u) | f(u) | 1 |
| g(v) | f(v) | 1 |
| g(w) | f(w) | 1 |
|
=0 |
| δ3 . g(u) |
μ1 . f(u) |
1 |
| δ3 . g(v) |
μ1 . f(v) |
1 |
| δ3 . g(w) |
μ1 . f(w) |
1 |
|
=0 |
 |