

Just to give you more ideas, examine this parallel scale nomogram:

Given a person's height and weight, the nomogram calculates that person's surface area. But notice the interesting thing: the two outer scales are also conversion scales! So it doesn't matter if the doctor's data is in feet or centimeters, the nomogram will still work. The center scale could have been a conversion scale as well, but I suppose they were trying to promote the metric system.
This is an important concept: combining several separate nomograms into one. A simple parallel nomogram can only handle three variables. By "chaining" or combining several nomograms more variables can be handles. For instance:

Given the amount of earth-moving to be done, this nomogram calculates the bucket size required on the front-end loader. This is actually two nomograms.
The first is composed of scales A, B, and C, while the second is composed of scales C, D, and E. As you see they share the C scale. The equation looks like A/B = C = E/D. To construct, two parallel scale nomograms are created, one for A/B=C and one for E/D=C, being sure to use the same functional moduli for each. Then the nomograms are superimposed with the C scales overlapping.
The resulting compound nomogram handles five variables instead of only three.
Also notice that the B, C, and E scales are conversion scales.
The nomogram is clearer if the scale on the edge is the one merged. But one can merge other scales if needed:
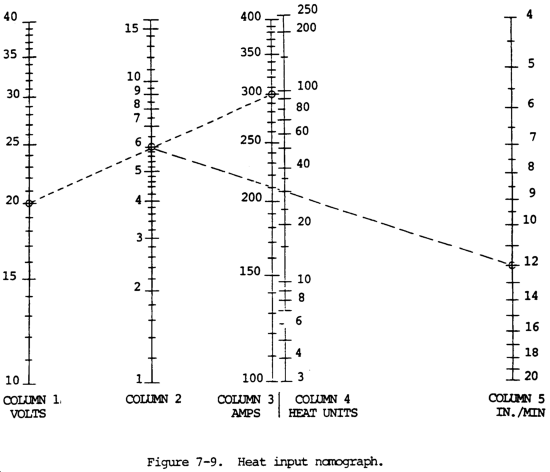
In this compound nomogram, the first nomogram is composed of scales Column 1, Column 2, and Column 3 while the second is composed of Column 2, Column 4 and Column 5. This can be confusing.
Taking the "use conversion scales for simple scales" idea one step further, we have this nomogram:
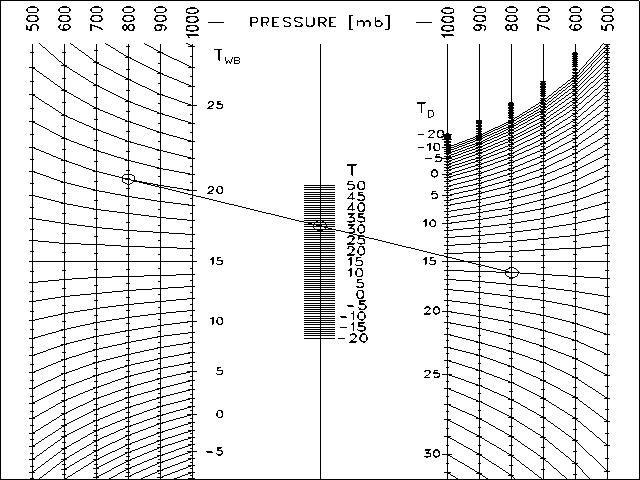
This is a standard parallel scale nomogram, but the two outer scales have been replaced by a family of scales. While this does make the nomogram more useful, it also introduces a new source of error. It is very important to use the corresponding outer scales (800 in the chart above). The nomogram will give an incorrect answer if for instance the 700 scale is used on the left and the 800 scale on the right.
I am unsure how to go about creating such a chart, but it will involve careful fiddling with the functional moduli.
Of course there is the danger of going overboard:

Sometimes, careful inspection of the resulting nomogram will reveal ways that it can be simplified. Consider the following ugly nomogram:

It calculates RV = (CV * CV_ADJ) + (B * 8 * MV_ADJ) where:
(CV_ADJ is actually seven value from Cos[+1.0º] to Cos[-1.0º] but you don't have to worry about that.)
As you can see by the two red and one green line, it requires laying the straight edge on the nomogram three times. That's too many.
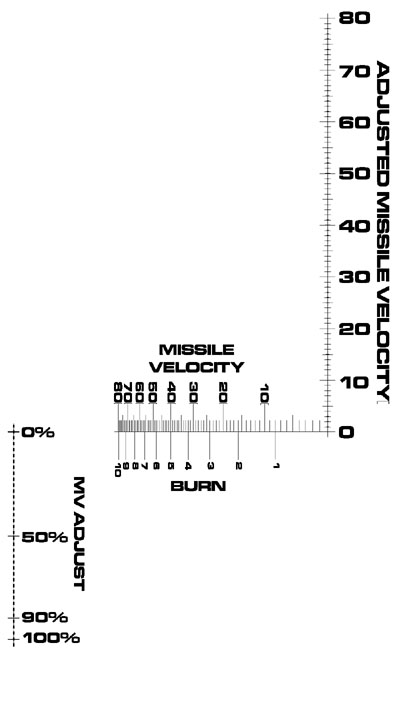
Look at the left side of the nomogram:
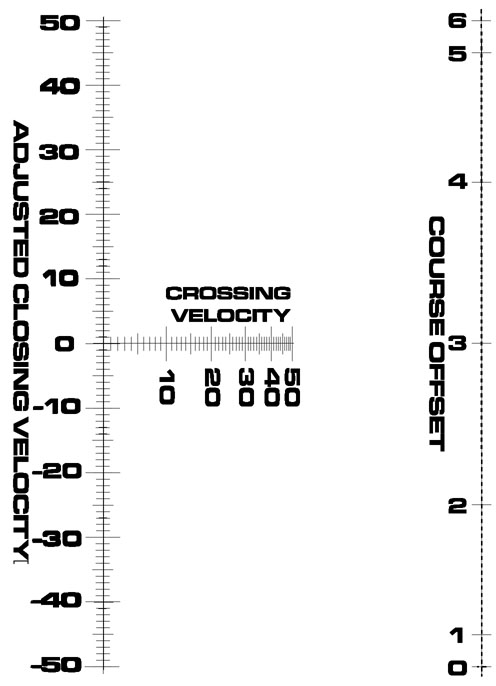
It calculates CV * CV_ADJ = ACV. But notice CV_ADJ. It only has seven values. Remember the family of scales above? We could replace the single Adjusted Closing Velocity scale with a set of seven scales. One scale would be CV * CV_ADJ where CV_ADJ=0, the next where CV_ADJ=1, and so on.
Taking it to extremes, we could squeeze it into one scale with seven sets of labels.
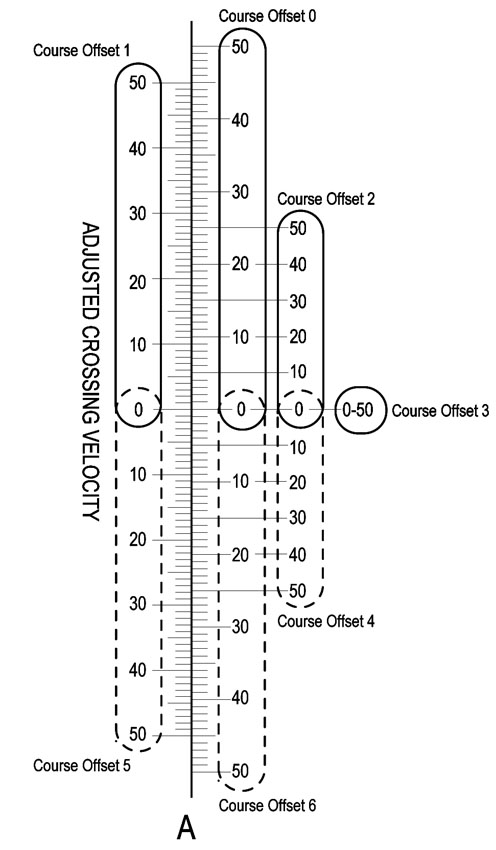
The even tick marks are on the right and the odd marks are on the left. Notice that this is sort of like a conversion scale, the marks on each side do NOT line up. My method of labeling could use some improvement, it is confusing. Above "Course Offset 4"'s label is its scale, enclosed in a dotted oval.
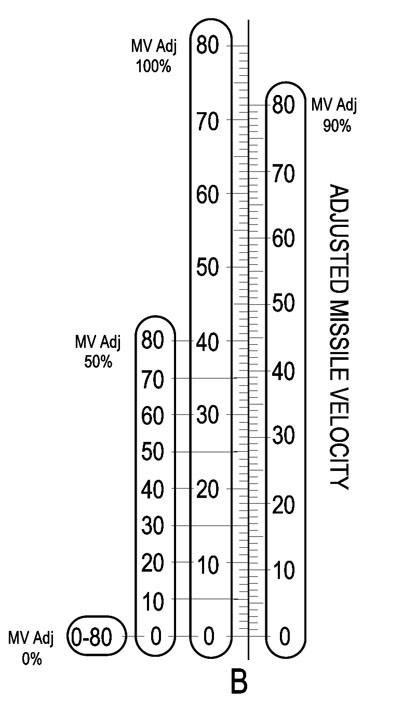
The same method can be used on the right side of the nomogram, transforming this:
into this:
The final nomogram looks like this:
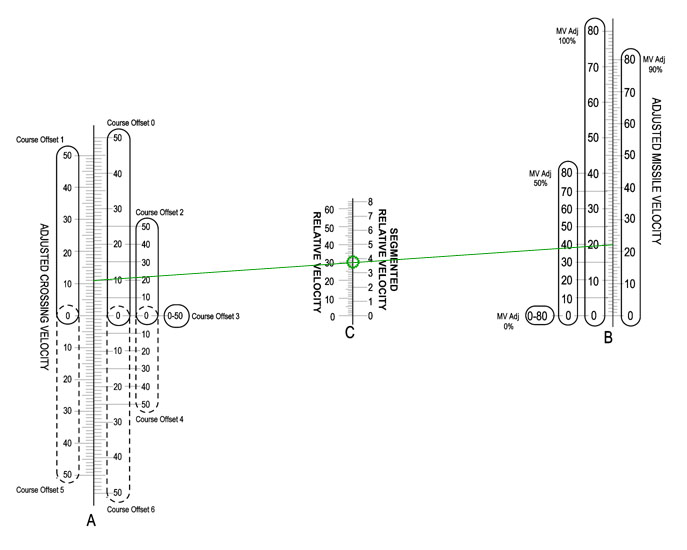
Note that it need only one straight-edge line (though you do have to take some care to read the correct scale legend on the right and left scales.)