
Are nomograms worth the trouble of learning how to construct them? Here are a couple examples that you can use to make your decision.

In the game, "pentaids" are a species of electronic counter-measure (ECM) missile. To calculate how much ECM the hostile incoming missiles have to cope with:
This can get tedious. Imagine going through this for every single missile volley.
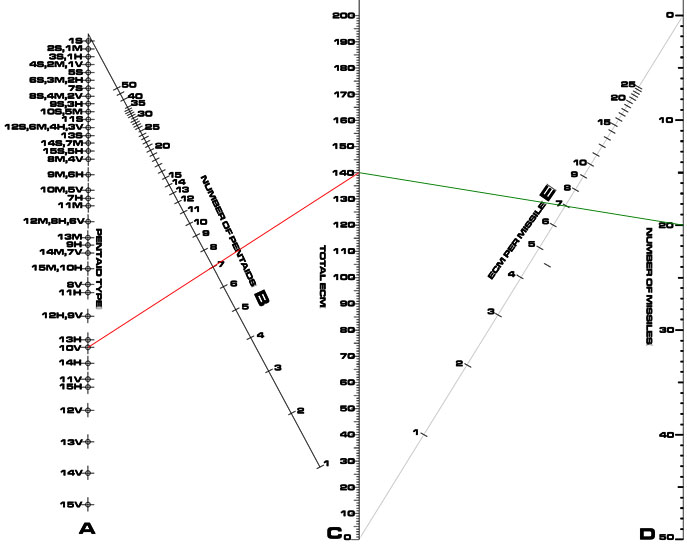
Now with the nomogram, lay a straight-edge from pentaid type (A scale) through the number of pentaids launched on the B scale (the red line in the diagram above). Note the total ECM on the C scale.
Now pivot the ruler on the total ECM so it crosses the number of missiles on the D scale (green line), and read the ECM per missile on the E scale (7 in the diagram above).
With nimble fingers on the straight-edge, the answer can be had in under two seconds.
Note how easy it is to work backwards. Given the number of incoming missiles and the available pentaid type, one can balance the desired ECM per missile with the number of pentaids to launch. Thus the player can use the nomogram to give a range of possible solutions from which the optimal one can be chosen. This is very difficult to do with an equation.
Also worthy of note is how the nomogram eliminates the need to look up the ECM of the pentaid type. It is automatically encoded in the nomogram.
This example was used in an earlier version of Ken Burnside's breakthrough game Attack Vector. (Take it from me, Buy this game.) Alas it was rendered obsolete by rules changes.
In the game, attacking a hostile starship with missiles has a steep learning curve, and requires referring to many separate tables. Once the process is learned, it is fairly easy. But it is still very time consuming, due to table lookups. The nomogram speeds up one particularly difficult part of the process.
In the nomogram, on the "Burn" scale, the setting for the missile's acceleration is chosen. The value for the "Segmented Relative Velocity" is more or less a constant for any given pair of mutually hostile starships. The "Time of Flight" is chosen, which is how much time the missile salvo spends traveling from launch point to the target. Segmented Relative Velocity cross referenced with Time of Flight on the grid will yield a point. Lay the straight-edge from this point to the Burn setting. Read the solution where the edge crosses the Deployment Range scale, revealing at what range the missiles should be launched at.
The red line on the nomogram demonstrates that if the Burn is 2, the Segmented Relative Velocity is 4 and the Time of Flight is 12, the Deployment range has to be 40.
Like all nomograms, this one can be used to solve for any of the four variables, so long as three are known. It can also be used to visualize the range of possible solutions.
If these two examples convince you that a nomogram or two is a worth while addition to your wargame, read on.