Triplanetary
designed by Marc. W. Miller and John Harshman
(1973, 1975, 1981) Game Designer's Workshop



Late breaking news: after about forty years of being out of print, Steve Jackson Games is bringing back Triplanetary by a Kickstarter.
This game has the One True way of managing vector movement in two dimensions (Ad Astra Game's Attack Vector has the One True way for three dimension).
The game is not only tons of fun and has lots of replay value, but it is educational as well. It teaches the players just how weird and strange space combat is when portrayed with scientific accuracy. But it does it painlessly, with rules so simple a grade-school child could learn them in a few minutes. The players will have so much enjoyment playing the game that they will not even notice they are learning Newtonian physics and vector addition.
Science fiction authors who want to get a feel for scientifically accurate space combat would do well to play a few games of Triplanetary.
The game is played on a hexgrid map covered with a piece of clear plastic or laminated. Grease pencil or other erasable markers are used to draw vectors on the map. A "vector" is a line with an arrow at the end, starting and ending in the center of a hex. The cardboard counter representing the spacecraft is placed on the last arrow.
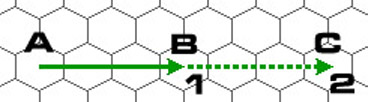
A spacecraft which moves from hex A to hex B in turn 1 will move to hex C in turn 2, provided that it does not accelerate due to gravity or burning fuel. This is good ol' Newton's First Law: a moving spacecraft will move for the rest of eternity at the same vector unless acted upon by some force. For instance, slaming into an asteroid.
To determine the spacecraft's future position next turn (hex C) examine the last vector (in this case, from hex A to hex B), start at the spacecraft's current position (hex B) and move in the same way as the last vector (three hexes to the right).
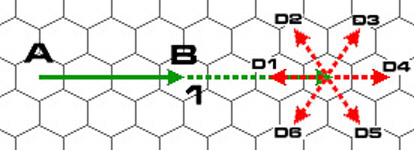
Triplanetary spacecraft can generally only burn one unit of fuel per turn. This changes the vector by one hex. Look at the diagram above. If the craft does nothing, next turn it will wind up in hex C at the end of the dotted green arrow. By burning one unit of fuel, the craft can change its vector's end point to D1, D2, D3, D4, D5 or D6.
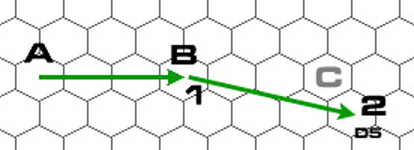
Say it burns one unit and chooses D5 as the new end point. Draw the new vector from B to D5. This is the new "last vector".
Now that wasn't hard, was it?
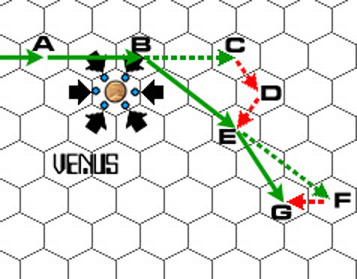
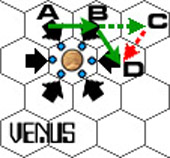
Gravity isn't much harder. The six black arrows around a planet are the "gravity hexes". On turn two, the spacecraft moves from A to B, passing through two of Venus' gravity hexes. (Note that one does not count any gravity hexes at the start of the vector, i.e., if there was a gravity hex in hex A it would be ignored)
On turn three, one would expect the ship to move to hex C. But the gravity passed through on turn two takes its toll. The first gravity hex moves the vector endpoint to hex D (that is, one hex in the same direction as the first gravity arrow), and the second moves it to hex E. Draw the new vector from B to E. Notice that the spacecraft moves through a third gravity hex.
In the same way, on turn four one would expect the ship to move to hex F, but the third gravity hex changes the vector end-point to G. Draw the new vector from E to G.
Please note that during all this the ship has burnt no fuel. All the change in course was due to the influence of gravity.
And now for the shining gem of elegance in this movement system: orbiting a planet.
In all other games, planetary orbits have to be taken care of by an ad hoc rule. But in the Triplanetary system orbits occur as a natural consequence of the existing rules.
Say the spacecraft is moving from hex A to hex B. Note it passed through one gravity hex (in hex B, you ignore any gravity hexes at vector start, remember?). In turn two, instead of moving to hex C, gravity alters the vector end point to hex D. Draw the new vector from B to D.
If you keep this up, you will realize that the spacecraft is in a one hex per turn orbit around Venus with no fuel or ad hoc rule required!
The game also teaches the limits of acceleration. If you are driving an automobile on Earth, and you accelerate up to 150 mph, you can still stop-on-a-dime by virtue of the friction from the road and the brakes. Triplanetary will quickly teach you that does not work in space. At all.
It happens to every first-time player. They spend about ten turns constantly accelerating. Their spaceship is moving at a speed of 10. About that time they look up and say "OH NO! I'm heading right for the edge of the map!" That's when they learn the hard way that if it takes ten turns to accelerate up to speed, it will take another ten turns to slow to a halt. There ain't no brakes in space, nor is there any road friction. You cannot come to a stop in only one turn.
The new player watches in horror as their spaceship goes streaking off the edge of the map.
There is also a bit of scientific accuracy in the combat system. Here on Earth it becomes harder to shoot your opponent with a gun as the range increases. This is true in Triplanetary as well. But in addition, the difficulty also increases as the relative velocity between you and your opponent increases.
Figuring the range between your ship and your opponent's ship easy. Like all other wargames you just count the hexes between the ships, not counting your hex but do count the hex your enemy is in (actually you figure the distance between your ship's location and the closest approach of your opponent's ship, but you get the idea).
You'd think figuring relative velocity would be very difficult, but you'd be wrong. It is also easy.
In an unused corner of the map, pick a hexagon. Using the same hexagon in both cases, draw the arrow vector of both your ship and your opponent's ship. Then count the hexes between the two arrowheads. That is the relative velocity. Again, do not count your arrowhead hex but do count your opponent's arrowhead hex. That was not hard, was it?
When you shoot your weapons at your opponent's ship, you roll a six-sided die. But from the die roll you have to subtract the range, and you have to subtract the relative velocity (actually the relative velocity minus 2, the first two relative velocity points are free. But you get the idea).
For those who own the game, there is some additional scenarios and material available at the Steve Jackson Games site.